등차수열을 설명하기 전에 먼저
수열은 일정한 규칙을 가진 수가 나열된 것을 얘기하는데,
예를 들어,
유명한 피보나치 수열은
첫째항이 1이고,
뒤에 나올 모든 항은
바로 앞 두 항의 더한 값이 되는 수열인데,
그림과 코드로 보면 이렇습니다.

public class Practice {
public static void main(String[] args) {
int[] Fibonacci = new int[10];
Fibonacci[1] = 1;
// 컴퓨터는 존재하지 않는 인덱스를
// 참조할 수 없기 때문에 인덱스 0이 아닌 인덱스 1에 값 1을 주고,
// 반복문은 2부터 시작합니다.
for (int i = 2; i < 10; i++) {
Fibonacci[i] = Fibonacci[i - 1] + Fibonacci[i - 2];
}
System.out.println(Arrays.toString(Fibonacci));
// 출력값 [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
}
}
그리고 오늘 이야기할 등차수열은,
어떤 숫자를 첫째 항으로 한다면,
첫째항에 같은 수를 계속 더하는 수열을
등차수열이라고 합니다.
같은 수를 더하기 때문에,
매 항마다 더해진 수 만큼의 차이가 있고,
이것을 공통된 차이, 공차라고 표현합니다.
즉, 공차를 가진 수열이란, 등차수열을 말합니다.
마찬가지로 그림과 코드로 간단하게 표현하면,

public class Practice {
public static void main(String[] args) {
int[] AP1 = new int[9];
int[] AP2 = new int[9];
int[] AP3 = new int[9];
// 등차수열 : arithmetic progression,
// 또는 arithmetic sequence
AP1[0] = 1;
AP2[0] = 2;
AP3[0] = 5;
// 각 등차수열의 첫째항 할당
for (int i = 1; i < 9; i++) {
AP1[i] = AP1[i - 1] + 1;
AP2[i] = AP2[i - 1] + 3;
AP3[i] = AP3[i - 1] - 3;
}
System.out.println(Arrays.toString(AP1));
// 출력값 [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
System.out.println(Arrays.toString(AP2));
// 출력값 [2, 5, 8, 11, 14, 17, 20, 23, 26]
System.out.println(Arrays.toString(AP3));
// 출력값 [5, 2, -1, -4, -7, -10, -13, -16, -19]
}
}
이제 만약 여기서,
첫째항과 공차만 알려주고,
첫째항부터 n번째 항까지의
누적합을 구하라고 한다면,
반복문으로 전부 다 더해도 값이 나오지만,
그것이 만약
엄청 많은 개수의 숫자를 가진 수열이라면,
일일이 더하는 데에 시간이 너무 오래 걸리게 됩니다.
그래서 등차수열의 합을 구하는 공식이 필요해졌는데,
일단 공식 먼저 쓰자면 아래와 같습니다.

이 공식을 이해하려면
등차수열의 일반항을 구하는 공식을 알아야 하므로,
그것도 아래에 적어보겠습니다.
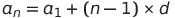
a1 은 첫째항,
d 는 공차,
n 은 일반항의 위치,
즉 n번째를 의미합니다.
따라서 an 은 n번째 항의 값이고,
이 n번째 항을 일반항 이라고 합니다.
공식을 무작정 외울순 없으니,
저 공식이 나오는 과정을 풀어보자면,
먼저 일반항 공식입니다.

그럼 이제
이 일반항 공식이 없이
일반항을 구하는 방법과,
일반항 공식을 사용해
일반항을 구하는 코드를 비교해 보여드리겠습니다.
public class Practice {
public static void main(String[] args) {
int a1 = 5;
int d = 3;
// 첫째 항을 5, 공차를 3 으로 가정.
int an = a1;
// 공차를 누적하기 위한 변수 초기화 및 초기값 할당.
for (int i = 1; i < 10; i++) {
// a1 으로 첫째항을 받았으니 반복문은 인덱스 1부터 시작.
an += d;
}
System.out.println(an);
// 출력값 32
// 아래는 등차수열의 일반항 공식을 이용한 결과입니다.
an = a1 + (10 - 1) * d;
System.out.println(an);
// 출력값 32
}
}시간복잡도가 O(n) 에서 O(1) 로 줄어들었습니다.
다음으로 일반항 공식을 이용한 합공식이고,
Sn 은 sum n 을 표현한 것이고,
l 은 an 이 지금 구하고자 하는 등차수열의 합의
마지막 값이라 last 에서 따왔습니다.

(글씨가 좀 많이 지저분해서 읽기 힘드셨다면 죄송합니다.)
이제 이 공식이 없이
그냥 공차를 누적해서 더한 코드와,
공식을 가지고 작성된 코드를 비교해서
아래에 보여드리겠습니다.
public class Practice {
public static void main(String[] args) {
int a1 = 5;
int d = 3;
// 첫째 항을 5, 공차를 3 으로 가정.
int an = a1;
int sumAP = a1;
// 합을 누적하기 위한 변수 초기화 및 초기값 할당.
for (int i = 1; i < 10; i++) {
// a1 으로 첫째항을 받았으니 반복문은 인덱스 1부터 시작.
an += d;
sumAP += an;
}
System.out.println(sumAP);
// 출력값 185
// 아래는 등차수열의 합 공식을 이용한 결과입니다.
sumAP = 10 * (2 * a1 + (10 - 1) * d) / 2;
System.out.println(sumAP);
// 출력값 185
}
}역시 마찬가지로,
시간복잡도가 O(n) 에서 O(1) 로 줄어들었습니다.
이처럼, 수학을 이해하고 잘 아는 것은,
나중에 충분히 응용이 가능해서,
특히 개발자에게 있어서
코드의 성능을 향상시키는데에
중요한 덕목인것 같습니다.
오늘 글은 여기서 마치겠습니다.
'알고리즘 및 개념 정리' 카테고리의 다른 글
| [JAVA] 카운팅 정렬(계수 정렬 : Counting Sort)에 대하여... (feat. 퀵 정렬은 왜 가장 많이 쓸까?) (0) | 2024.05.02 |
|---|---|
| [JAVA] 정렬을 코드로 구현하기. (삽입, 선택, 버블, 셸, 퀵, 합병, 힙, 기수) (0) | 2024.03.30 |
| 향상된 for문, for-each 문에서 주의할 점. (0) | 2024.03.09 |
| imos 법 (いもす 法, imos 法) 에 대한 간략한 소개 및 설명. (0) | 2024.03.09 |
| 2진, 8진, 10진, 16진법과 상호 간의 변환 (0) | 2024.03.04 |